El cálculo de los coeficientes combinatorios entra de lleno en la filosofía de grandes estructuras que se calculan mediante interacciones locales.

     Podemos simularlo mediante un autómata bidimensional con las siguientes reglas:

• Si una celda se encuentra en el borde superior, su valor permanece constante.
• Si una celda no se encuentra en la situación 1.,su valor es igual a la suma de los valores de las celdas diagonales superiores.

     Así pues, partiendo de una celda inicial con el valor 1, se tiene:

y tras cinco iteraciones:

     Una regla que produce estructuras muy interesante es la regla de la antimayoría; consiste en lo siguiente:

     "Una célula nace o permanece viva si entre una y cuatro (ambos inclusive) de sus células adyacentes se hallan vivas".

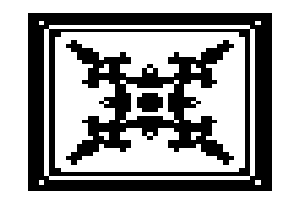
     Esto provoca fenómenos de propagación a partir de pocas células vivas iniciales, conserva simetrías e impide la excesiva concentración de células vivas. De hecho es un autómata que produce resultados muy vistosos y muy distintos; las siguientes figuras corresponden a pasos consecutivos, a partir de una única celda central:

Estado tras varias iteraciones	Siguiente estado
Siguiente estado	Siguiente estado
Siguiente estado	Siguiente estado
Siguiente estado	Siguiente estado
Siguiente estado	Siguiente estado

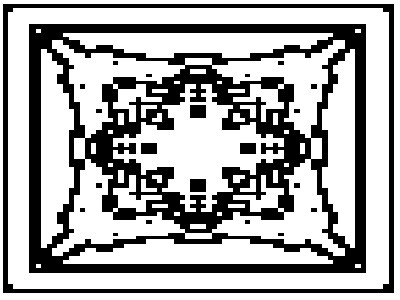
     Las figuras son semejantes, pero se va obteniendo cada vez más detalle. Podemos ver esto en la siguiente figura, que representa un número de iteración mucho mayor.